A quick guide on PID controllers
I got a bit excited in my F1 article, so I thought I'd better give a quick explanation of what a PID controller is. PID stands for Proportional, Integral, Differential. A controller can just have a P term so it would be a proportional controller. It can also have I and D terms, but it doesn't have to have both.
Introduction
To explain about controllers, I'm going to use the example of a central heating system. I'm British so we don't typically have air con, just heating.
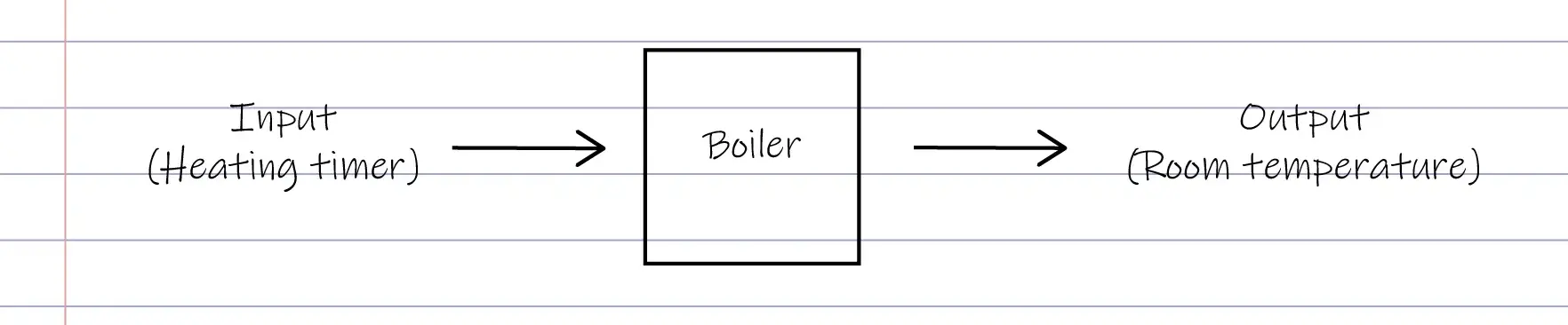
When I bought my house, it had a 25+ year old boiler and no thermostat. The only control was the timer. When the timer says to turn on, the boiler turns on, no matter what temperature the house is. It stays on as long as the timer tells it to be on.
This system didn't have any feedback; there was no way of monitoring the room temperature and telling (feeding back to) the boiler.
A system with no feedback is called 'open loop'.
Bang-bang controllers
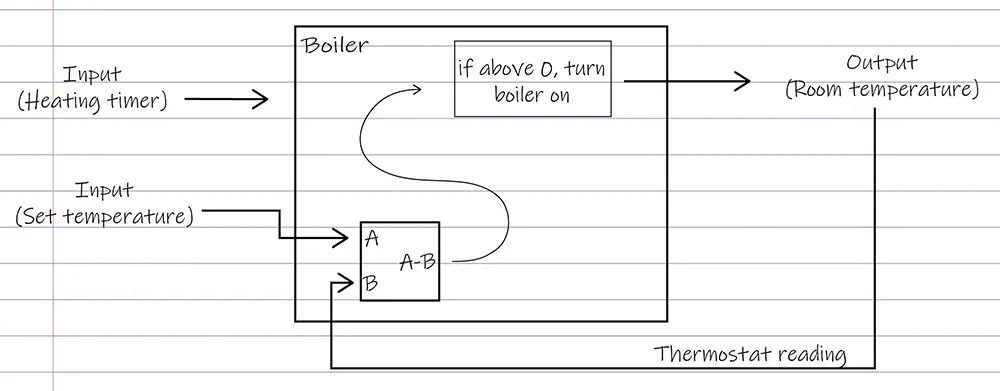
Because I had just bought my first house, I didn't have the money for frivolities like heating. I acted like a thermostat - when the house got warm enough, I went upstairs to the timer box and manually turned the heating off. When it cooled down, I went back upstairs and turned it on again.
I was basically being a thermostat. I had a set temperature (the temperature I wanted the room to be) and I could sense the room temperature. When the room temperature was lower than the set temperature, I turned the boiler on. When the room temperature was higher than the set temperature, I turned the boiler off.
The boiler only has two states: on or off.
This is called a bang-bang controller, because the boiler goes BANG, BANG between its two states instead of moving gently between them.
Proportional controllers
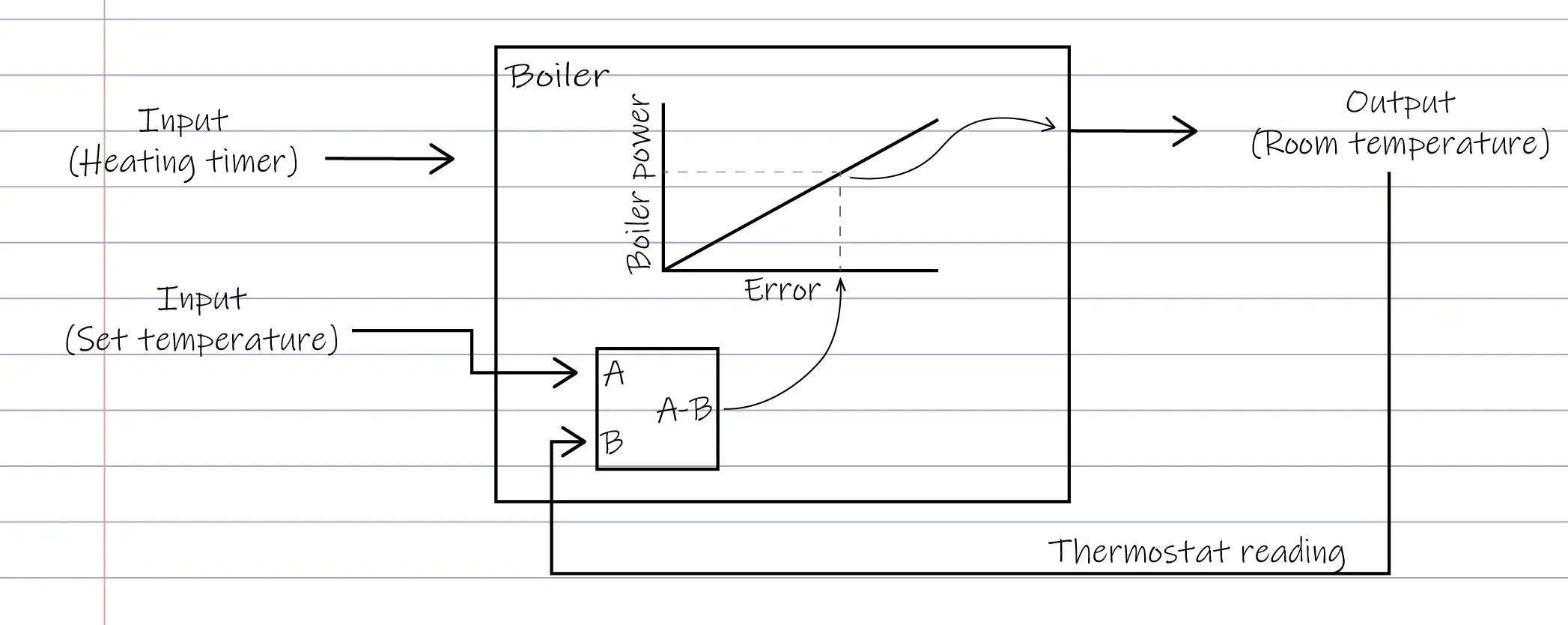
Once I was feeling a bit more flush (and I decided I was sick of my terrible heating system) I bought myself a nice new boiler. Like it isn't fuel efficient to always drive with your foot to the floor, it isn't efficient to always run your boiler at full power. Instead, modern boilers can vary how much effort they are putting in, like how you can vary how much you press the accelerator pedal.
In this situation, then, the boiler needs to know how different the set temperature and the room temperature are. If they're a long way apart, the boiler turns on more so that it can warm the room up faster. If the room is almost the right temperature, the boiler calms down. That way it saves you money.
(It would also stop it overshooting. The radiators stay warm even after the boiler has turned off, right? So if the boiler carried on blasting away at high power until the second the room temperature hit the set temperature, the radiators would still be hot and would carry on heating the room. That means the boiler has used more gas than it needed to get the temperature to where you wanted it)
Anyway. This is a proportional controller. Because the power level of the boiler is proportional to the "error term" - that is, the difference between the set point and the actual point.
Integral term
Integrals are how you find the area under a curve (i.e., between the line and zero) of a graph.
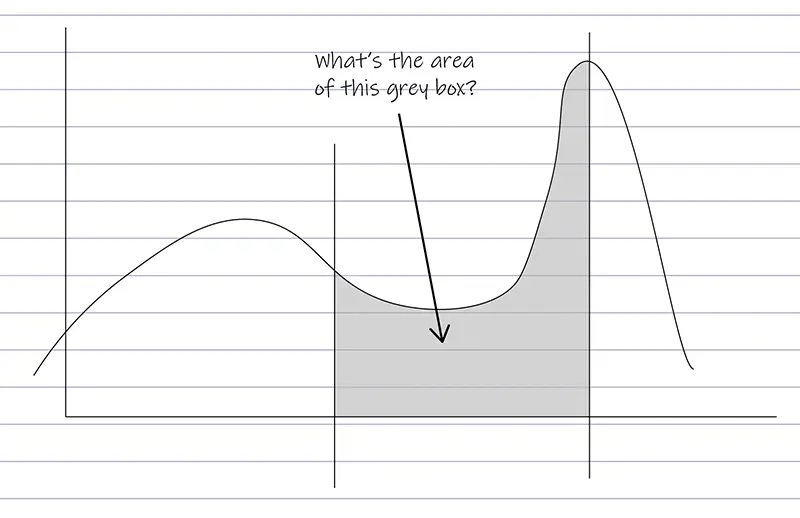
The error over time can be plotted as a graph.
Therefore the integral term looks at the area under the curve of the error graph. If the area is bigger, the integral term gets bigger.
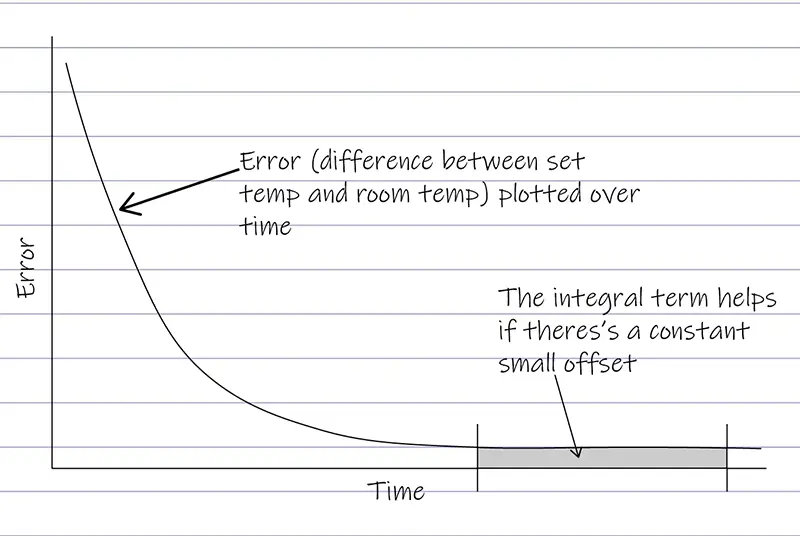
In our boiler example, maybe the boiler has a minimum level of error before it actually turns on. If it got stuck and just slightly too chilly, though, that would be annoying. So if the integral term gets too big, even though the actual error is very small, it will make the boiler turn on and heat up a bit more.
Differential term
Differentiation is how you find out the slope of a line on a graph.
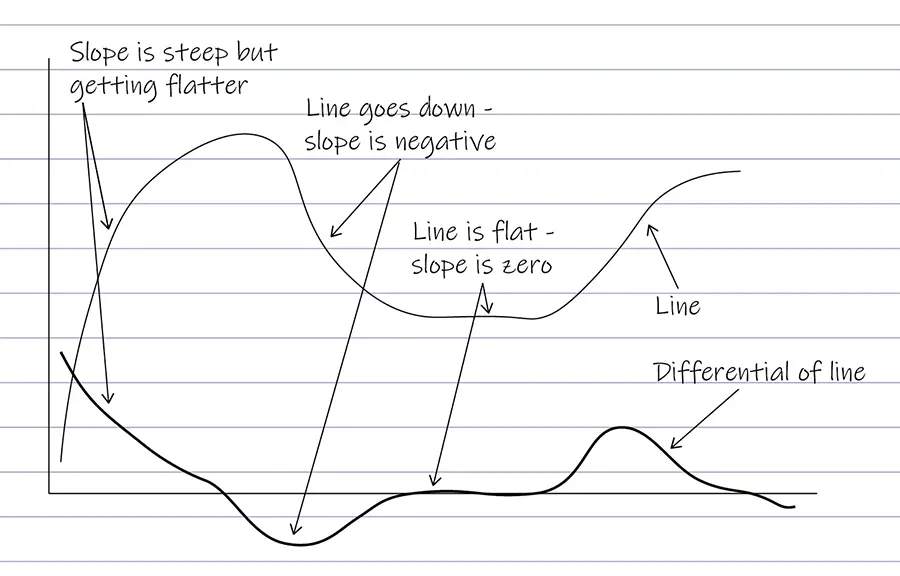
Looking again at the plot of the error over time, we can see that at first the error term is changing quickly. The differential would therefore be very big. However, because the error is decreasing the differential is negative. As the line flattens out, the differential ends up at zero. So it's basically the same shape but upside down.

A differential term sort of works to moderate the integral and proportional terms. If your house was better insulated than the boiler manufacturer expected, turning the boiler on to 50% would make the house heat up much faster than in a badly insulated house. The error would decrease much more quickly, so the differential term would be bigger (and more negative). It would say to the boiler, hey, just relax. Don't try so hard!"
So why is PID not AI?
Because the controller isn't doing anything thinking, or working out for itself. Someone at Valliant, or Worcester, or wherever, sat down and worked out that if the error is 5 degrees, the boiler needs to work at 42% capacity in an average house (numbers pulled out of thin air).
You could make a boiler controller with computational intelligence. You'd give it a house and let it do something at random. If it was cold and it turned the heating on, you'd give it a good mark. If it was cold and it did nothing, you'd give it a bad mark. Over time, the controller would 'learn' what values it should have.
Conclusion
Lets be honest, no boiler is going to have any more than proportional control. But I hope it's helped you understand what a PID controller is.

